1 神经网络中的激活函数activation function

1.1 引入激活函数概念

神经网络的基本构成单元是神经元。 

在一文中使用的神经元模型为

这个神经元模型是较为简化的基本神经元模型。还有一种理论模型包含有激活函数和偏置项的神经元模型

1943年McCulloch 和 Pitts 提出了一种神经元模型，这也就是McCulloch-Pitts神经元模型：

该神经元模型中的数学公式表示为?(∑?_??_?  + ?)，f为激活函数

激活函数：引入非线性激活因素，避免∑?_??_?  + ?纯线性组合的缺陷，提高了模型的表达力，使模型具有更好的区分度。

1.2 常见的激活函数

常用的激活函数有 relu、sigmoid、tanh 等

 

1.2.1 激活函数relu

（1）tf中表达式： tf.nn.relu() 

（2）数学表达式

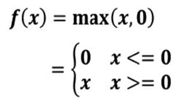
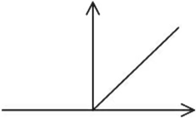
（3）函数图像

1.2.2 激活函数sigmoid

（1）Tensorflow中表达式： tf.nn.sigmoid() 

（2）数学表达式

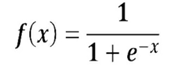
（3）函数图像

1.2.3 激活函数tanh

（1）Tensorflow中表达式： tf.nn.tanh() 

（2）数学表达式

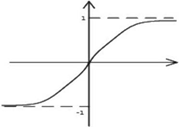
（3）函数图像

2 损失函数loss

损失函数：前向传播生成的预测值 (y) 与 标签 (y_) 之间的差距。

NN的优化目标：获得具有最小loss的神经网络模型。在训练神经网络时，就是通过不断改变神经网络中的权重参数、偏置量等参数，使损失函数不断减小，从而训练出更高准确率的神经网络模型。

常用的损失函数有均方误差mse(Mean Squared Error)、自定义和交叉熵ce(Cross Entropy)等

2.1 均方误差mse

2.1.1 均方误差的公式

假设有n个样本，其对应标签为y_，经神经网络计算的预测值为y。

（1）均方误差定义：

预测值y与标签y_差值平方和的平均数

（2）数学公式

（3）Tensorflow公式

loss_mse = tf.reduce_mean(tf.square(y_ - y))

2.1.2 均方误差的实例应用

拟合预测酸奶日销量的函数；便于准确预测销量后指导产量（最佳 销量=产量）。

假设预测酸奶日销量为y，影响日销量的两个因素x1、x2。并有采集的每日因素 x1、x2 和销量 y_ 历史数据。

（在实际上，并没有酸奶相关数据，所以需要拟造一套数据集并进行神经网络训练）

# 第一步 导入模块，生成数据集import tensorflow as tfimport numpy as npBATCH_SIZE = 8SEED = 23455rdm = np.random.RandomState(SEED)# 拟为用32组数据训练神经网络,有2个特征参数X = rdm.rand(32,2)# 生成数据集标签，# rdm.rand()函数返回值在0~1之间，确切地讲位于0.1~1之间，# rdm.rand()/10.0-0.05的结果相对x1、x2来讲低一个量级，# 这里表示仅对x1+x2的值微调。Y_ = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X]# 第二步 定义前向传播过程# placeholder为喂入数据集及数据标签占位x = tf.placeholder(tf.float32, shape=(None, 2))y_ = tf.placeholder(tf.float32, shape=(None, 1))# 生成前向传播时所需权重参数赋值，标准差stddev=1# 由于该神经网络为一层，所以仅赋一个权重参数即可w1= tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))# 矩阵运算，两个矩阵乘积y = tf.matmul(x, w1)# 第三步 损失函数及反向传播过程# 选用均方误差MSE作为损失函数loss_mse = tf.reduce_mean(tf.square(y_ - y))# 选用梯度下降法作为权重优化函数train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss_mse)#第四步 生成会话，训练STEPS轮with tf.Session() as sess:    # 全局变量初始化    init_op = tf.global_variables_initializer()    sess.run(init_op)    # 进行循环优化权重参数，20000轮    STEPS = 20000    for i in range(STEPS):        # start为0、8、16、24        start = (i*BATCH_SIZE) % 32        # 每次喂入BATCH_SIZE数据量        end = start + BATCH_SIZE        # 执行数据训练过程，train_step权重优化函数，喂入数据集及对应标签        sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})                # 每循环500次打印一下权重参数训练效果，        if i % 500 == 0:            print("After %d training steps, w1 is: " % (i))            print(sess.run(w1), "\n")            # 计算损失函数值，观察损失函数随训练次数的变化趋势            totle_mse = sess.run(loss_mse, feed_dict={x: X, y_: Y_})            print(totle_mse, "\n")    print("Final w1 is: \n", sess.run(w1))

运行

After 0 training steps, w1 is: [[-0.80974597] [ 1.4852903 ]] 0.6557005 After 500 training steps, w1 is: [[-0.46074435] [ 1.641878  ]] 0.35731 After 1000 training steps, w1 is: [[-0.21939856] [ 1.6984766 ]] 0.23248056 After 1500 training steps, w1 is: [[-0.04415595] [ 1.7003176 ]] 0.17040439 After 2000 training steps, w1 is: [[0.08942621] [1.673328  ]] 0.13303667 After 2500 training steps, w1 is: [[0.19583555] [1.6322677 ]] 0.10693912 After 3000 training steps, w1 is: [[0.28375748] [1.5854434 ]] 0.08706193 After 3500 training steps, w1 is: [[0.35848638] [1.5374471 ]] 0.071270935 After 4000 training steps, w1 is: [[0.4233252] [1.4907392]] 0.05849066 After 4500 training steps, w1 is: [[0.48040032] [1.4465573 ]] 0.048065245 After 5000 training steps, w1 is: [[0.5311361] [1.4054534]] 0.0395331 After 5500 training steps, w1 is: [[0.57653254] [1.367594  ]] 0.032540925 After 6000 training steps, w1 is: [[0.6173259] [1.3329402]] 0.02680777 After 6500 training steps, w1 is: [[0.65408474] [1.3013425 ]] 0.022105861 After 7000 training steps, w1 is: [[0.68726856] [1.2726018 ]] 0.018249318 After 7500 training steps, w1 is: [[0.7172598] [1.2465004]] 0.015086038 After 8000 training steps, w1 is: [[0.74438614] [1.2228196 ]] 0.012491369 After 8500 training steps, w1 is: [[0.7689325] [1.2013482]] 0.0103631 After 9000 training steps, w1 is: [[0.79115146] [1.1818888 ]] 0.00861741 After 9500 training steps, w1 is: [[0.81126714] [1.1642567 ]] 0.0071855206 After 10000 training steps, w1 is: [[0.8294814] [1.1482829]] 0.0060110046 After 10500 training steps, w1 is: [[0.84597576] [1.1338125 ]] 0.0050475756 After 11000 training steps, w1 is: [[0.8609128] [1.1207061]] 0.00425734 After 11500 training steps, w1 is: [[0.87444043] [1.1088346 ]] 0.0036091362 After 12000 training steps, w1 is: [[0.88669145] [1.0980824 ]] 0.0030774516 After 12500 training steps, w1 is: [[0.8977863] [1.0883439]] 0.0026413407 After 13000 training steps, w1 is: [[0.9078348] [1.0795243]] 0.002283624 After 13500 training steps, w1 is: [[0.91693527] [1.0715363 ]] 0.001990209 After 14000 training steps, w1 is: [[0.92517716] [1.0643018 ]] 0.0017495381 After 14500 training steps, w1 is: [[0.93264157] [1.0577497 ]] 0.0015521289 After 15000 training steps, w1 is: [[0.9394023] [1.0518153]] 0.0013901924 After 15500 training steps, w1 is: [[0.9455251] [1.0464406]] 0.0012573693 After 16000 training steps, w1 is: [[0.95107025] [1.0415728 ]] 0.0011484219 After 16500 training steps, w1 is: [[0.9560928] [1.037164 ]] 0.0010590521 After 17000 training steps, w1 is: [[0.96064115] [1.0331714 ]] 0.0009857531 After 17500 training steps, w1 is: [[0.96476096] [1.0295546 ]] 0.0009256217 After 18000 training steps, w1 is: [[0.9684917] [1.0262802]] 0.0008763098 After 18500 training steps, w1 is: [[0.9718707] [1.0233142]] 0.00083585805 After 19000 training steps, w1 is: [[0.974931 ] [1.0206276]] 0.00080267614 After 19500 training steps, w1 is: [[0.9777026] [1.0181949]] 0.0007754609 [Finished in 11.7s]

为了便于对比观察，对比头2次和尾2次的数据

After 0 training steps, w1 is: [[-0.80974597] [ 1.4852903 ]] 0.6557005 After 500 training steps, w1 is: [[-0.46074435] [ 1.641878  ]] 0.35731 ……After 19000 training steps, w1 is: [[0.974931 ] [1.0206276]] 0.00080267614 After 19500 training steps, w1 is: [[0.9777026] [1.0181949]] 0.0007754609

此时耗时Finished in 11.7s

也可以将损失函数计算 totle_mse = sess.run(loss_mse, feed_dict={x: X, y_: Y_}) 放在 if i % 500 == 0 外面，耗时 [Finished in 18.2s]，这间接说明两种情况 loss_mse 的执行次数是不一样的。

在 if i % 500 == 0 外面时，每次 for i in range(STEPS) 都会运行一次，而在其里面是每隔500次运行一次。

 

注意（没有完全想明白）：

 

1 loss_mse = tf.reduce_mean(tf.square(y_ - y)) 2 totle_mse = sess.run(loss_mse, feed_dict={x: X, y_: Y_})3 print(totle_mse, "\n")

loss_mse的计算代码中仅和 y_ 值有关，若将第二行代码修改为

totle_mse = sess.run(loss_mse, feed_dict={y_: Y_})

会报错

InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'Placeholder' with dtype float and shape [?,2]     [[Node: Placeholder = Placeholder[dtype=DT_FLOAT, shape=[?,2], _device="/job:localhost/replica:0/task:0/device:CPU:0"]()]]

开始意为是Y_值的求算与X有关

Y_ = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X]

对Y_值进行修改，变成与X无关的变量。结果还是报同样的错误。

 

又仔细观察了报错说明（InvalidArgumentError ）和位置（下图两个位置）。

初步推断可能是在进行会话运行时，必须对所有初始化变量中的placeholder 进行 feed a value

 2.2 自定义误差

采用均方误差时，只是建立产量-销量的关系，当且仅当成本 = 利润时，该关系模型才有可能实现利润最大化。

• 预测多了( y ≥ y_ )，损失成本COST
• 预测少了( y ＜y_ )，损失利润PROFIT

若建立成本-产量-销量-利润关系模型，实现利润最大化，同时人具体核算的任务量就会降低。

 

2.2.1 建立数学模型

自定义损失函数

（1）建立初步模型

 （2）模型细化

 

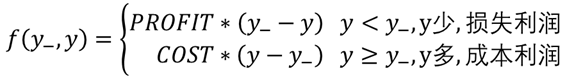
 （3）转化成Tensorflow语句

loss = tf.reduce_sum(tf.where(tf.greater(y,y_), COST*(y-y_), PROFIT*(y_-y)))

 

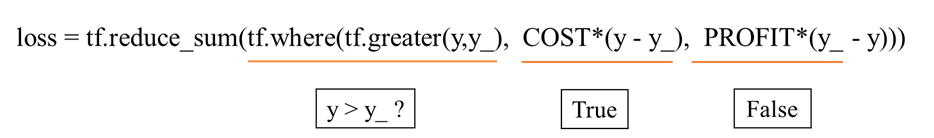
2.2.2 自定义损失函数的实例应用

一个单位量的酸奶成本COST为1元，利润PROFIT为9元

预测少一个单位量的酸奶则损失利润9元

预测多一个单位量的酸奶则损失利润1元

此时生成的函数应该是往多了的预测，也即倾向于 ‘ 微多 ’ 

注：下列代码仅修改了损失函数部分，在引入库部分增加了常量COST、PEROFIT赋值代码。 

# 第一步 导入模块，生成数据集import tensorflow as tfimport numpy as npBATCH_SIZE = 8SEED = 23455COST = 1PROFIT = 9rdm = np.random.RandomState(SEED)# 拟为用32组数据训练神经网络,有2个特征参数X = rdm.rand(32,2)# 生成数据集标签，# rdm.rand()函数返回值在0~1之间，确切地讲位于0.1~1之间，# rdm.rand()/10.0-0.05的结果相对x1、x2来讲低一个量级，# 这里表示仅对x1+x2的值微调。Y_ = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X]# 第二步 定义前向传播过程# placeholder为喂入数据集及数据标签占位x = tf.placeholder(tf.float32, shape=(None, 2))y_ = tf.placeholder(tf.float32, shape=(None, 1))# 生成前向传播时所需权重参数赋值，标准差stddev=1# 由于该神经网络为一层，所以仅赋一个权重参数即可w1= tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))# 矩阵运算，两个矩阵乘积y = tf.matmul(x, w1)# 第三步 损失函数及反向传播过程# 选用自定义损失函数作为条件loss_user_def = tf.reduce_sum(tf.where(tf.greater(y,y_), COST*(y-y_), PROFIT*(y_ - y)))# 选用梯度下降法作为权重优化函数train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss_user_def)#第四步 生成会话，训练STEPS轮with tf.Session() as sess:    # 全局变量初始化    init_op = tf.global_variables_initializer()    sess.run(init_op)    # 进行循环优化权重参数，20000轮    STEPS = 20000    for i in range(STEPS):        # start为0、8、16、24        start = (i*BATCH_SIZE) % 32        # 每次喂入BATCH_SIZE数据量        end = start + BATCH_SIZE        # 执行数据训练过程，train_step权重优化函数，喂入数据集及对应标签        sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})                # 每循环500次打印一下权重参数训练效果，        if i % 500 == 0:            print("After %d training steps, w1 is: " % (i))            print(sess.run(w1), "\n")            # 计算损失函数值，观察损失函数随训练次数的变化趋势            totle_mse = sess.run(loss_user_def, feed_dict={x: X, y_: Y_})            print(totle_mse, "\n")    print("Final w1 is: \n", sess.run(w1))

运行结果（略），W1最终值 ‘ 略大’；成本低，利润高，多产些、浪费点无所谓。

[[1.0225189] [1.0416601]]

若将数值更变

COST = 9PROFIT = 1

运行结果（略），W1最终值 ‘ 略小’；成本高，利润低，少产些、浪费点会增加成本。

[[0.9661967 ] [0.97694933]]

2.3 交叉熵ce(Cross Entropy)

交叉熵表示两个概率分布之间的距离。

交叉熵越大，概率间距越远，两概率分布越相异；

交叉熵越小，概率间距越近，两概率分布越相似；

 （1）数学表达式：

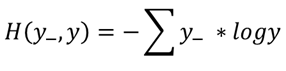
（2）Tensorflow语句

ce = - tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-12, 1.0)))

备注：

为了保障tf.log有意义，当 y 值小于1e-12时，将 y 值 clip 为 1e-12，当 y 值大于 1 时，将 y 值 clip 为 1 。

示例：

在二分类问题方面，已知标准答案为y_ = (1,0)，现有两个预测结果y1 = (0.6,0.4)、y2 = (0.8,0.2)，那个结果更接近标准答案呢？

根据交叉熵ce公式计算得：

H1((1,0),(0.6,0.4)) = -(1*log0.6 + 0*log0.4)  ≈ -(-0.222 + 0) = 0.222

H2((1,0),(0.8,0.2)) = -(1*log0.8 + 0*log0.2)  ≈ -(-0.097 + 0) = 0.097

所有y2预测更准。

2.4 softmax 函数

2.4.1 函数的基本释义

摘录于

 softmax函数（也称为归一化指数函数）是逻辑函数的一种推广。

它能将一个含任意实数的 K 维向量 z "压缩"到另一个 k 维实向量 σ(z) 中，使得每一个元素的范围都在 (0,1) 之间，并且所有元素的和为 1 ，该函数（softmax函数）的形式通常按下面的式子给出：

 softmax函数实际上是有限项离散概率分布的梯度对数归一化。因此，softmax函数在包含多项逻辑回归、多项线性判别分析、朴素贝叶斯分类器和人工神经网络等的多种基于概率的多分类问题方法中都有着广泛应用。特别地，在多项逻辑回归和线性判别分析中，函数的输入是从 k 个 不同的线性函数得到的结果，而样本向量 x 属于第 j 个分类的概率为：

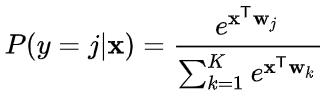
这可以被视作 k 个线性函数 x   |→   x^Tw₁, . . . , x   |→   x^Tw_k Softmax函数的复合（x^Twxw）

2.4.2 函数的示例及代码诠释

输入向量 [1,2,3,4,1,2,3] 对应的Softmax函数的值为  [0.024,0.064,0.175,0.475,0.024,0.064,0.175] 。输出向量中拥有最大权重的项对应着输入向量中的最大值“4”。这也显示了这个函数通常的意义：对向量进行归一化，凸显其中最大的值并抑制远低于最大值的其他分量。

代码：

下面是使用Python进行函数计算的示例代码：

import mathz = [1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0]z_exp = [math.exp(i) for i in z]  print(z_exp)  # Result: [2.72, 7.39, 20.09, 54.6, 2.72, 7.39, 20.09] sum_z_exp = sum(z_exp)  print(sum_z_exp)  # Result: 114.98 softmax = [round(i / sum_z_exp, 3) for i in z_exp]print(softmax)  # Result: [0.024, 0.064, 0.175, 0.475, 0.024, 0.064, 0.175]

Python使用numpy计算的示例代码:

import numpy as npz = np.array([1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0])print(np.exp(z)/sum(np.exp(z)))

 

 2.4.3 Tensorflow中的实现形式

该部分是这个函数在本小节的重点，2.4.1 和 2.4.2 是辅助理解过程。

ce = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1))cem = tf.reduce_mean(ce)

 2018-10-28 23:28:31